Si quieres aprender correctamente las partes del circulo, en este espacio vamos a explicar concretamente sus elementos y además un par de ejercicios.
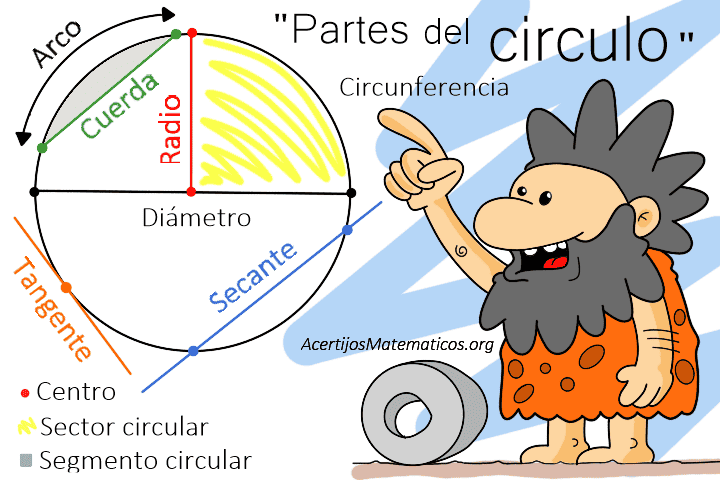
La figura del día de hoy es de las más importantes y es que de ella se desprende una de las grandes invenciones de la humanidad, "la rueda", la que facilitó la movilidad, la exploración y por lo tanto el desarrollo de las culturas.
Seguro que si prestas atención y miras a tu alrededor podrás encontrarlo como un elemento en la construcción o el diseño de varios artículos, herramientas y objetos que utilizas en tu día a día.
Cuales son las partes que lo conforman
Debemos recordar que los conocimientos básicos siempre son importantes y es que, tanto si eres docente o estudiante, saber distinguir cuales son todas las partes que lo conforman pude abrir las puertas al entendimiento de ejercicios y áreas de interés más avanzadas. Por ejemplo, como profesor se puede motivar a los alumnos, con argumentos, sobre cuales son las profesiones que tienen en su base estos conocimientos como arquitectura, diseño, ingenierías etc.
Centro
El centro es el punto equidistante (que tiene las misma distancia) de todos los puntos de la circunferencia. Se denota comúnmente con la letra "O",
- Aunque también se puede encontrar representado con la "C", dependiendo la bibliografía que uses.
El radio
Es el segmento (es decir, tramo de una recta) que une el centro del círculo con cualquier punto de la circunferencia. Se representa con la letra "r".
- Por lo tanto podemos deducir que si trazamos varios de ellos dentro de un mismo circulo, todos los radios medirán lo mismo.
El diámetro
Es un segmento que une dos puntos de la circunferencia y tiene como característica que siempre pasa por el centro. Su símbolo es "∅", aunque es común denotarlo simplemente con la "d".
- De lo anterior decimos que el diámetro, es en consecuencia, s el doble del radio
- Formula (d= 2r).
La circunferencia (perímetro)
Se trata de la línea curva y cerrada cuyos puntos están a la misma distancia del centro.
- Es el contorno del círculo, es decir su perímetro, por eso se suele denotar como "P".
- Su formula es: P=2π • r
- (dos veces el número "pi" multiplicado por el radio)
Cuerda
Es un segmento que une dos puntos de la circunferencia sin pasar necesariamente por el centro.
- La longitud de la cuerda se calcula con la formula
- L = 2 (√ r2 - d2 )
Donde:
- L= Es la longitud de la cuerda
- r= Es el radio del circulo
- d= Distancia del centro a la cuerda
Arco
Es cualquier porción de la circunferencia comprendida entre dos puntos y su longitud se expresa en grados o radianes. Las podemos clasificar en:
- Arco menor: Es el arco más corto entre dos puntos de la circunferencia.
- Arco mayor: Es el arco más largo entre dos puntos de la circunferencia.
- Semicircunferencia: Es un caso especial de arco en el que los dos puntos extremos son los extremos de un diámetro, dividiendo la circunferencia en dos partes iguales.
La formula para encontrar la cuerda es:
- En grados:
L = (0/360°) (2π r)
- En radianes
L= rθ
Donde:
θ es el ángulo central en grados o radianes.
r es el radio del círculo.
"Cada arco tiene asociada una cuerda, que es el segmento recto que une sus extremos"
Sector circular
Es la región del círculo limitada por dos radios y el arco comprendido entre ellos.
Segmento circular
Es la parte del círculo limitada por una cuerda y el arco que une sus extremos.
La tangente
Es una recta que toca la circunferencia en un solo punto.
Ejemplos y aplicaciones
- Óptica y reflexión: En espejos y lentes, los rayos de luz reflejados siguen la dirección de la tangente en el punto de incidencia.
- Física y mecánica: En el movimiento circular, la velocidad de un objeto en un círculo es siempre tangente a su trayectoria.
- Geometría y trigonometría: Las tangentes son fundamentales para definir funciones trigonométricas y resolver problemas geométricos.
La secante
Es una recta que corta la circunferencia en dos puntos
Ejercicios que involucran al circulo
Ya que el rango de dificultades y grados en los que pueden utilizarse estos casos es muy amplio, los ejercicios que vamos a proponer tienen como propósito ejemplificar algunas posibilidades, pero que pueden ser útiles para formular tareas más específicas.
Menciona tres lugares u objetos de la vida diaria que consideres se utilizaron algunas de estas partes par su diseño y explica.
Se tiene un circulo con un radio de 10 cm y una cuerda que se encuentra a 6cm del centro. ¿Cuál será la longitud de dicha cuerda?.
Si un círculo tiene radio de 10 cm y el arco es subtendido por un ángulo de 60. Encontrar la longitud del arco?.
Cómo se llama el único punto de contacto donde la tangente toca la circunferencia?.
Como hemos mencionado, cada uno de estos ejemplos son casos que dan para profundizar y desde luego queda mucho por aprender. Sin embargo creemos que es suficiente para comenzar a estudiarlo.
