Números griegos
Aquí te mostramos y explicamos cuales son los números griegos con ejemplos claros, desde su historia, escritura, símbolo y también su valor.

Como es bien conocido y ya hemos estudiado en otras ocasiones el mundo griego antiguo ha tenido una gran influencia a la hora sentar las bases que contribuyeron a dar forma a las diferentes ciencias y disciplinas de las que actualmente nos beneficiamos tanto. Sabias que tenían una manera particular de expresar cada número, aunque en la actualidad y en el resto del mundo han perdido presencia, es interesante estudiarlos y al hacerlo entender la magnitud del conocimiento y exactitud que podían representar desde ya hace tanto tiempo.
Sistema de numeración griega
En la antigua Grecia tenían un sistema numérico propio que utilizaban para contar y hacer cálculos. Este sistema se basaba en letras del alfabeto griego para representar a cada uno de los números.
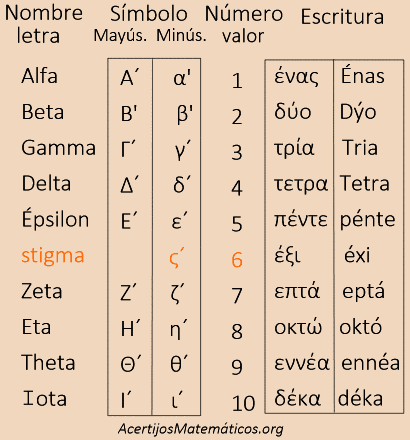
Eran utilizados para realizar desde las tareas cotidianas que requerían representar cantidades o el conteo como en el comercio y hasta tareas como la construcción y en toda actividad que requería el uso de cálculos matemáticos. Este sistema empleaba para ello las letras del ya conocido alfabeto griego para denotar valores numéricos. A diferencia del sistema decimal posicional que usamos hoy en día, donde el valor de un dígito depende de su posición en relación con otros dígitos, el sistema este sistema de numeración asignaba valores numéricos específicos a cada letra de su alfabeto.
"No confundir el nombre de la letra con la escritura del número que representa, como se muestra en la tabla de arriba".
Unidades
Se usaban las primeras letras del alfabeto griego para representar los números del uno al 9 exceptuando al "seis", para el cual se empleaba el símbolo "stigma ".
| Nombre de la letra |
Símbolo Mayús. Minús. |
Valor |
| Alfa | A´ α´ | 1 |
| Beta | Β´ β´ | 2 |
| Gamma | Γ´ γ´ | 3 |
| Delta | Δ´ δ´ | 4 |
| Epsilon | Ε´ ε´ | 5 |
| Stigma | ϛ | 6 |
| Zeta | Ζ´ ζ´ | 7 |
| Eta | Η´ η´ | 8 |
| Theta | Θ´ θ´ | 9 |
Números del 1 al 10
Además se debe colocar una muesca o acento en la parte superior derecha de cada símbolo para indicar que se trata de un número y no de una letra.
Letras o símbolos añadidos
Cabe señalar que el alfabeto griego tiene 24 letras, sin embargo para poder representar cada cifra se tuvo que añadir tres símbolos más, los cuales eran vocablos antiguos y corresponden a:
| Nombre de la letra | Símbolo | Valor |
| Stigma | ϛ´ | 6 |
| Qoppa | Ϙ´ | 90 |
| Sampi | ϡ´ | 900 |
Para evitar confusiones y dependiendo de la fuente donde encuentres una cifra en este sistema, debes prestar atención a la letra que se ha empleado e identificar si han usado la forma mayúscula o minúscula de ella. Aunque comúnmente y en los ejemplos que mostraremos usaremos la minúscula.
Múltiplos de diez - decenas
Para contar o formar las decenas se empleaban en orden las letras que siguen, incluyendo "Qoppa" para el 90, como ya se menciono anteriormente. De igual manera se debe colocar el acento en la parte superior derecha para diferenciarlos de las letras.
| Nombre de la letra |
Símbolo Mayús. Minús. |
Valor |
| Iota | Ι´ ι´ | 10 |
| Kappa | Κ´ κ´ | 20 |
| Lambda | Λ´ λ´ | 30 |
| Mu | Μ´ μ´ | 40 |
| Nu | Ν´ ν´ | 50 |
| Xi | Ξ´ ξ´ | 60 |
| Omicrón | Ο´ ο´ | 70 |
| Pi | Π´ π´ | 80 |
| Qoppa | Ϙ´ ϙ´ | 90 |
Números del 1 al 100
Para escribir cantidades hasta el 99 se formaban combinando estas letras en función de su valor numérico y obteniendo de una suma la cifra deseada. Por ejemplo:
ι´ε´= (iota + epsilon) = (10+15) = 15
κ´ζ´ = (kappa + zeta) = (20 + 7) = 27
λ´θ´ = (lambda + theta) = (30+ 9) = 39
Recuerda que estamos usando la versión en minúscula de cada símbolo en estos ejemplos para expresar nuestras cantidades.
Múltiplos de cien - centenas
Para escribir las cantidades por centenas vamos a utilizar las letras restantes del alfabeto, incluyendo el vocablo "sampi" para el 900. También deben tener el acento.
| Nombre de la letra |
Símbolo Mayús. Minús. |
Valor |
| Rho | Ρ´ ρ´ | 100 |
| Sigma | Σ´ σ´ | 200 |
| Tau | Τ´ τ´ | 300 |
| Upsilon | Υ´ υ´ | 400 |
| Phi | Φ´ φ´ | 500 |
| Chi | Χ´ χ´ | 600 |
| Psi | Ψ´ ψ´ | 700 |
| Omega | Ω´ ω´ | 800 |
| Sampi | ϡ' | 900 |
Números del 1 al 1000
De igual manera vamos a obtener estas cantidades con el principio de la suma de cada valor siguiendo el orden de centena, decena, y unidad. Por ejemplo
ρ´ν´δ´= (rho + nu + delta) = (100+ 50 + 4) =154
σ´ν´ζ´ = (sigma + nu + zeta )(200 + 50 + 7) = 257
τ´π´α´ = (tau + pi + alfa)(300 + 80 + 1) =381
Millares
Para los correspondientes a los "miles" volvemos a utilizar las primeras letras, pero esta vez añadiremos una coma en el lado izquierdo inferior de cada símbolo para indicar de que se trata de una cantidad por mil.
| Nombre de la letra |
Símbolo Mayús. Minús. |
Valor |
| Alfa | ,A ,α | 1000 |
| Beta | ,Β ,β | 2000 |
| Gamma | ,Γ ,γ | 3000 |
| Delta | ,Δ ,δ | 4000 |
| Epsilon | ,Ε ,ε | 5000 |
| Stigma | ,ϛ | 6000 |
| Zeta | ,Ζ ,ζ | 7000 |
| Eta | ,Η ,η | 8000 |
| Theta | ,Θ ,θ | 9000 |
Números del 1 al 9999
Siguiendo el mismo principio tendremos que organizar cada letra por millares, centenas, decenas y unidad, para poder expresar estas cantidades de manera correcta. Tenemos los siguientes ejemplos:
,α ψ´λ´β´= (,alfa + psi+ lambda + beta)=(1000 + 700 + 30 + 2)=1732
,β χ´ ϙ α = (,beta + chi + qoppa + alfa)=(2000 + 600 + 90 + 1)= 2691
,γ ϡ' κ´ η =(,gamma + sampi + kappa + eta)=(3000 + 900 + 20 + 8)= 3928
Observa como la primer letra lleva consigo una coma a su izquierda, para indicar que son miles. Hemos puesto el nombre escrito para ejemplificar y hacerlo más entendible, aunque de no recordar cual es cada una, utiliza las tablas aquí expuestas para localizarlas.
Como veras entender la naturaleza y la composición de los números cuando han sido escritos en el sistema griego no es tan complicado. Basta con conocer su estructura y el valor asignado a cada letra para poder leer o escribir nuestras propias cifras.
Tarea propuesta - Escribir la cantidad propuesta
Escribir con este sistema de numeración la cantidad propuesta: El profesor del colegio debe proponer a la clase una serie de cantidades, luego de presentar y explicar algunos ejemplos, se acordará un tiempo para llevar acabo la dinámica.Pasado este tiempo los alumnos podrán dar sus respuestas y detallar como es que llegaron a ella.
