Partes de una ecuación
Aquí te explicaremos a detalle cuales son las partes de una ecuación de diferentes grados y con algunos ejemplos útiles para el colegio.
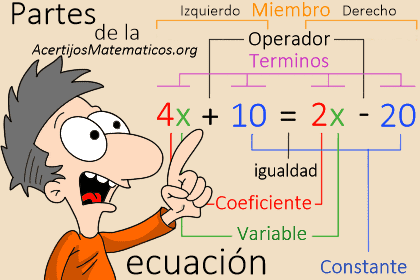
Las encontramos en muchas materias y son útiles para el estudio de las diversas ciencias, por lo que entender las ecuaciones, su forma y sus elementos, es parte fundamental para el desarrollo y la resolución de ejercicios y problemas que no se limitan solo a las matemáticas. Cada elemento tiene características y particularidades que vamos a detallar de forma clara y de una vez
4x + 10 = 2x - 20
En el ejemplo de la imagen encontramos una ecuación con variables o incógnitas en ambos lados. Por lo que, para resolverla debemos acomodar (siguiendo las reglas de signos y operaciones) ubicando variables de un lado y constantes del otro, para poder reducir las expresiones y finalmente encontrar el valor de "X".
Básicamente se compone de tres partes principales:
Pero dentro de cada una de ellas se puede encontrar otras de las cuales vamos a hablar y entrar en detalle más abajo.
Por ejemplo, en la ecuación:
2x+3=7
Lado o miembro izquierdo: Es la expresión que se encuentra a la izquierda del signo igual. Por lo general, representa una cantidad desconocida o variable que estamos tratando de encontrar.
El lado izquierdo es: 2x+3
Igualdad o Signo igual (=): Indica que las expresiones a ambos lados de la ecuación son iguales entre sí. Sin importar que elementos contengan, siempre debe mantenerse esta igualdad (si se resuelve correctamente).
Lado o miembro derecho: Es la expresión matemática que se encuentra a la derecha del signo igual. Por lo general, representa el valor conocido o la cantidad con la que se está comparando la cantidad desconocida en el lado izquierdo
El lado derecho es simplemente: 7
Para conocer más de ellas es necesario incorporar el concepto del grado al estudiarlas, por que te invito a continuar leyendo para averiguarlas.
Partes de una ecuación lineal - de primer grado
Estas se caracterizan por que la potencia mayor que poseen sus variables es igual a 1. Recuerda que no es necesario escribir el uno arriba de la x o la y, siempre serán de primer grado si no tienen un exponente escrito.
Este ejemplo tiene solo una variable.
ax + b = C
5x + 6 = 0
Este otro caso cuenta con dos variables.
ax+ by = C
2x + 9y = 7
Variables: Las ecuaciones lineales tienen una o más variables o incógnitas, que son letras que representan cantidades desconocidas. Las más utilizadas son "x", "y", "z". Para evitar confusiones.
En el segundo ejemplo las variables son x, y.
Coeficientes: Son los números que multiplican a las variables.
Los coeficientes son el 2 y el 9.
Constantes: Suele representarse con la C. Son los números que no están asociados con ninguna variable en la expresión y cuyo valor conocemos por que esta bien definido, también incluyen al cero.
La constante es 7.
Operadores matemáticos: Pueden contener operadores matemáticos como suma (+) y resta (-) entre los términos. También la multiplicación (no confundir con la variable X ) o la división y desde luego todas las demás.
En el segundo ejemplo, encontramos un solo operador que es la suma.
La igualdad: Que como ya vimos indica que el miembro derecho es igual al izquierdo.
Partes de una ecuación cuadrática - de segundo grado
Para identificar y definir cada uno de los elementos que hay en ellas debemos conocer primero cual es la forma general de una ecuación cuadrática. Esta se llama así precisamente por que la potencia de mayor valor que contiene es 2 (al cuadrado).
ax2 + bx + c = 0
Por ejemplo, en esta ecuación de segundo grado: Vemos que la forma es la misma solo que ahora ya colocamos números en ella.
8x2 + 4x + 6 = 0
Término cuadrático: ax2 Es el término que contiene la variable elevada al cuadro x2 y donde a es el coeficiente del término cuadrático.
El término cuadrático es 8x2 y su coeficiente es 8.
Término lineal: bx Es el término que contiene la variable elevada a la primera potencia x1 donde b es el coeficiente del término lineal.
El término lineal es 4x y para este el coeficiente es 4.
Término constante: c Es el término independiente de la variable, es decir, que no contiene ninguna variable.
La constante es simplemente 6, ya que su valor no cambia.
Igualdad: En este caso indica que todo el lado izquierdo es igual a cero.
Actividad propuesta en clase: Define y localiza cada parte.
Antes de comenzar con la resolución en forma de ejercicios, debemos asegurarnos de conocer y entender cada parte. Por lo que el profesor del colegio o tutor debe escribir una serie de ejemplos para que el grupo ubique los nombres de cada elemento que hay en ellas.
Luego y después de un tiempo previamente establecido, podrán decir en voz alta al grupo las que identificaron en algún ejemplo y justificar con argumentos el porque de su respuesta.
